Evaluating Limits Algebraically Pdf
By When your pre-calculus teacher asks you to find the limit of a function algebraically, you have four techniques to choose from: plugging in the x value, factoring, rationalizing the numerator, and finding the. The best place to start is the first technique.
3,001 Business & Sales Letters is a deluxe version of Easy Letters. You get its entire collection of award-winning letters, plus 901 new sales letters that will help you sell more with attention-getting messages and persuasive sales copy. See all the letter topics. Writeexpress 3001 business sales letters 2017 and torrent 2017 full. You will with our 500 letter-writing tutorials! • Find the that fits your needs and copy it directly into Microsoft Word or your favorite word processor. Torrent Contents. 3001 business letters. 3001 bus letters. WriteExpress.txt 1,215 B. New telugu moviestelugu movie 2017 latest telugula 0s.
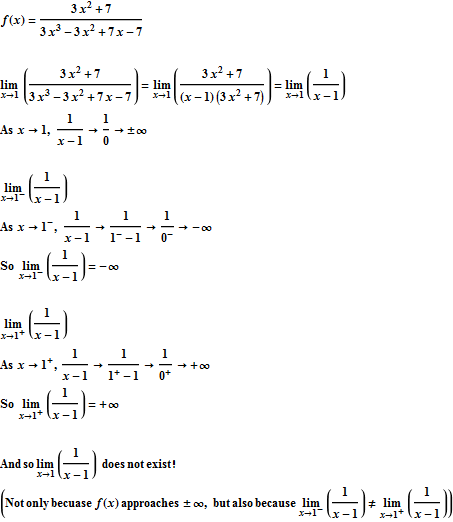
You may only use this technique if the function is continuous at the x value at which you are taking the limit. If the function is undefined at this x value, you must move on to the other techniques to simplify your function so that you can plug in the approached value for x. Find the limit by plugging in the x value The first technique for algebraically solving for a limit is to plug the number that x is approaching into the function. If you get an undefined value (0 in the denominator), you must move on to another technique. But if your function is continuous at that x value, you will get a value, and you’re done; you’ve found your limit!
Evaluating Limits Algebraically Worksheet Pdf
For example, with this method you can find this limit: The limit is 3, because f(5) = 3 and this function is continuous at x = 5. Find the limit by factoring is the method to try when plugging in fails — especially when any part of the given function is a polynomial expression. Say you’re asked to find this limit: You first try to plug 4 into the function, and you get 0 in the numerator and the denominator, which tells you to move on to the next technique. The quadratic expression in the numerator screams for you to try factoring it. Notice that the numerator of the previous function factors to ( x – 4)( x – 2). The x – 4 cancels on the top and the bottom of the fraction. This step leaves you with f( x) = x – 2.
You can plug 4 into this continuous function to get 2. If you graph this function, it looks like the straight line f( x) = x – 2, but it has a hole when x = 4 because the original function is still undefined there (because it creates 0 in the denominator). The figure illustrates this. If, after you’ve factored the top and bottom of the fraction, a term in the denominator didn’t cancel and the value that you’re looking for is undefined, the limit of the function at that value of x does not exist (which you can write as DNE). For example, this function factors as shown: The ( x – 7) on the top and bottom cancel.
Finding Limits Algebraically
So if you’re asked to find the limit of the function as x approaches 7, you could plug 7 into the cancelled version and get 11/8. But if you’re trying to find the limit DNE, because you’d get 0 on the denominator. This function, therefore, has a limit anywhere except as x approaches –1.
Infinite Limits. Lim x→2+x−6 x−2, when evaluated by substitution, produces −4 0, which is the same form as 1 0. The numerator is clearly negative near x=2 (as we learned when we evaluated). As x approaches 2 from the right, we have x>2, which implies x−2>0, so the denominator is positive. Limits (Evaluating) You should read Limits (An Introduction) first. Quick Summary of Limits. Evaluating Limits 'Evaluating' means to find the value of (think e-'value'-ating) In the example above we said the limit was 2 because it looked like it was going to be. But that is not really good enough!
Find the limit by rationalizing the numerator The third technique you need to know to find limits algebraically requires you to rationalize the numerator. Functions that require this method have a square root in the numerator and a polynomial expression in the denominator. For example, say you’re asked to find the limit of this function as x approaches 13: Plugging in numbers fails when you get 0 in the denominator of the fraction. Factoring fails because the equation has no polynomial to factor. In this situation, if you multiply the numerator and denominator by the conjugate of the numerator, the term in the denominator that was a problem cancels out, and you’ll be able to find the limit: • Multiply the top and bottom of the fraction by the conjugate.
The conjugate of the numerator is Multiplying through, you get this setup: FOIL the numerator to get which simplifies to x – 13 (the middle two terms cancel and you combine like terms from the FOIL). • Cancel factors. Canceling gives you this expression: The ( x – 13) terms cancel, leaving you with this result: • Calculate the limits. When you plug 13 into the function, you get 1/6, which is the limit. Find the limit by finding the lowest common denominator When you’re given a complex rational function, you use the fourth and final algebraic limit-finding technique. The technique of plugging fails, because you end up with a 0 in one of the denominators.